Sliding Window Attention

Longformer - The Long-Document Transformer

In this post, we take a deep dive into Sliding Window Attention that allowed transformers to have long context length. We do this with the help of animations and also implement it from scrath in PyTorch code.

LLM
Author

Aman Arora

Published

July 4, 2024

As part of this blog post, we will look take a deep dive into Sliding Window Attention (SWA) that was introduced as part of the Longformer architecture (Beltagy, Peters, and Cohan (2020)), and also understand how it’s implemented in PyTorch!

When I first started looking into sliding window attention, below tweet kind of summarises my journey. O thought it’s pretty complicated and hard to implement. But, as is usual with many things, the more time you spend on it, the easier it gets.

Having spent some time on digging through the LongerFormer implementation in Huggingface, I have realised that it’s really not that hard. But, first, let’s understand what sliding window attention really is and how it’s different from full-attention.

1 Introduction

Figure 1: Comparing the full self-attention pattern and the configuration of attention patterns in Longformer

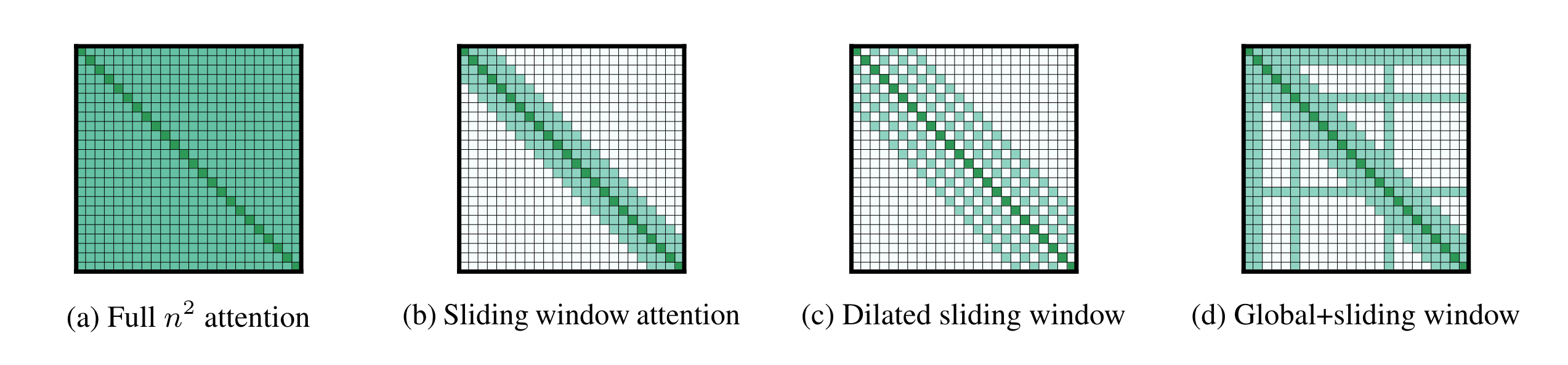
The above image from the Longformer paper (Beltagy, Peters, and Cohan (2020)), summarises the difference between Full \(n^2\) attention & Sliding window attention.

In the traditional sense, \[ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V \]

Each token in the Query vector \(Q\) can attend to all tokens in the Key vector \(K\).

But, this leads to a computational complexity of \(O(n^2)\). As a result, memory requirements grow by a factor of \(n^2\) for a sequence of length \(n\).

This limits the traditional Transformer architecture from having long context length. The solution is to use Sliding window attention where each token in the Query vector \(Q\) only attends to it’s neighbouring tokens with an overlap of window length \(w\).

So, a token at position \(i\) in \(Q\), can attend to tokens in range \((i-w, i+w)\) in \(K\).

2 Matrix multiplication using torch.einsum

Figure 2: Visualisation of matrix multiplication from http://matrixmultiplication.xyz/

Before we get started with Sliding Window Attention, let’s implement \(Q.K^T\) matrix multiplication with the help of torch.einsum.

For a refresher/introduction to matrix multiplication and torch.einsum, I recommend the below amazing lecture by Jeremy Howard.

To implement, \(Q.K^T\) using Einstein summation is as easy as doing:

import torch 
q = torch.arange(1, 9).reshape(4,2)
k = torch.arange(1, 9).reshape(4,2)
out = torch.einsum('xd,yd->xy', q, k)
out.shape
torch.Size([4, 4])
More on torch.einsum

I would recommend the readers to play around with torch.einsum notation, try writing simple matrix multiplications and see the results for yourself to get an intuition.

x = torch.tensor([7,6,5,4]).unsqueeze(1)
y = torch.arange(start=1, end=5).reshape(1,4)
torch.einsum("ij, jk", x,y)

As for why torch.einsum('xd,yd->xy', q, k) represents \(Q.K^T\), here’s a detailed explanation:

  • “xd, yd -> xy” specifies the operation: x and y represent the outer dimensions (4x4) & d represents the inner dimension for multiplication (2, in this case)
  • The result is a 4x4 tensor where each element is the dot product of a row from \(q\) with a column from \(k\)

Before moving on the next section, I would recommend that the readers make sure that they can correlate below outputs with Figure 2.

q,k.T,out
(tensor([[1, 2],
         [3, 4],
         [5, 6],
         [7, 8]]),
 tensor([[1, 3, 5, 7],
         [2, 4, 6, 8]]),
 tensor([[  5,  11,  17,  23],
         [ 11,  25,  39,  53],
         [ 17,  39,  61,  83],
         [ 23,  53,  83, 113]]))

Great, now that we know what Sliding Window Attention is, and how to use einstum summation to do matrix multiplication, we are ready to see how Sliding Window Attention can be implemented in PyTorch.

3 Sliding window attention in PyTorch

From Appendix A of the LongFormer paper (implementation detail, text slightly modified to match implementation):

Longformer-chunks only supports the nondilated case. It chunks Q and K into overlapping blocks of size \(2*w\) and overlap of size \(w\), multiplies the blocks, then mask out the diagonals. This is very compute efficient because it uses a single matrix multiplication operation from PyTorch, but it consumes \(2x\) the amount of memory a perfectly optimized implementation should consume because it computes some of the zero values. Because of the compute efficiency, this implementation is most suitable for the pretrain/finetune case. We didn’t find the increase in memory to be a problem for this setting.

To explain further, to achieve the same results as Figure 1 (b), it is possible to divide the Query \(Q\) and Key \(K\) vectors to chunks of size \(2*w\), where \(w\) represents the window length or the overlap size. Then, we can perform the attention operation and get scores by doing \(Q.K^T\) within the chunks themselves! This way, it’s very efficient as it only involves a single matrix multiplication operation.

Let’s see how the above translates to PyTorch code. Let’s define a query \(q\) and a key \(k\) vector of batch size 1, sequence length 8 and embedding size 768.

import torch
q = torch.randn(1, 8, 768)
k = torch.randn(1, 8, 768)

Let’s assume a query and key vector of batch size 1, sequence length 8 and embedding size of 768. These can be converted to overlapping chunks using the _chunk function below.

Figure 3: Chunking overview

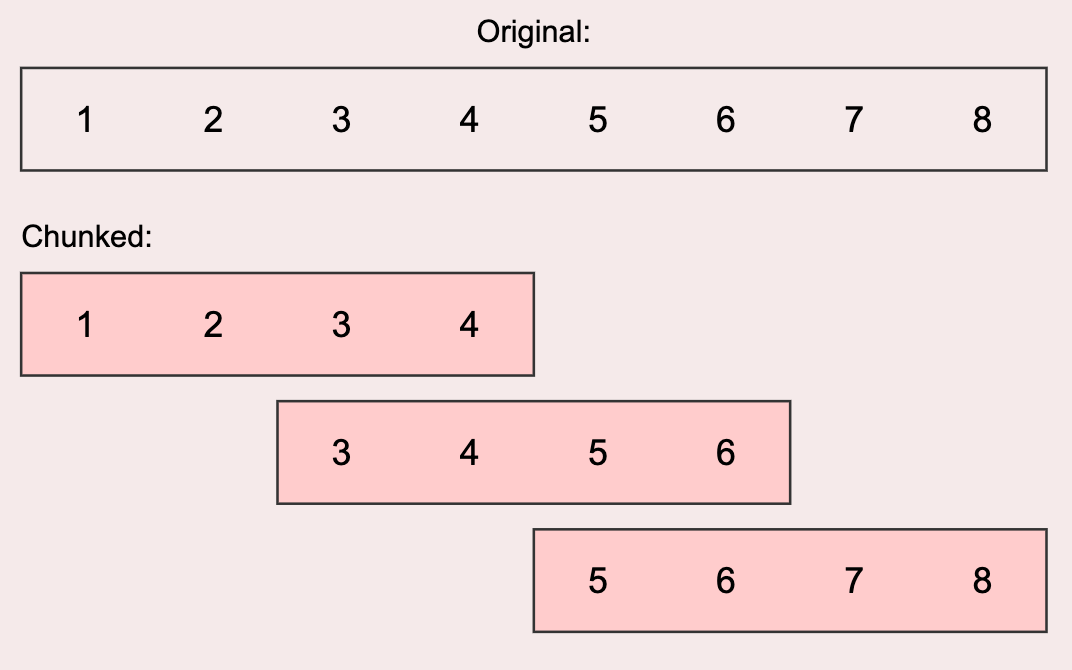
Given a reference image above, in PyTorch implementation, we don’t really need to create three separate vectors, but instead we can create one called overlapping_chunks with the right shape and overlap.

def _chunk(hidden_states, window_overlap):
    """convert into overlapping chunks. Chunk size = 2w, overlap = w"""
    chunk_size = [
        hidden_states.size(0), #bs
        torch.div(hidden_states.size(1), window_overlap, rounding_mode="trunc") - 1, #n_chunks
        window_overlap * 2,
        hidden_states.size(2),
    ]

    overlapping_chunks = torch.empty(chunk_size, device=hidden_states.device)
    for chunk in range(chunk_size[1]):
        overlapping_chunks[:, chunk, :, :] = hidden_states[
            :, chunk * window_overlap : chunk * window_overlap + 2 * window_overlap, :
        ]
    return overlapping_chunks

Let’s check the key & query shapes after chunking. In total we have 3 chunks, where the chunk size is 4.

query = _chunk(q, window_overlap=2)
key   = _chunk(k, window_overlap=2)
query.shape, key.shape
(torch.Size([1, 3, 4, 768]), torch.Size([1, 3, 4, 768]))

Finally, we can now perform sliding window attention using torch.einsum. This is where the matrix multiplication of between query \(Q\) and key (transposed) \(K^T\) occurs using torch.einsum.

diagonal_chunked_attention_scores = torch.einsum("bcxd,bcyd->bcxy", (query, key)) 
diagonal_chunked_attention_scores.shape
torch.Size([1, 3, 4, 4])

By performing matrix multiplication \(Q.K^T\) within chunks, we have succesfully replicated Figure 1 (b) in PyTorch. Had we not created any chunks, and done our matmul operation on all of \(Q\) and \(K^T\), it would have been equivalent to Figure 1 (a).

And that’s really it! This is all the magic behind Sliding Window Attention from the Longformer architecture. (Beltagy, Peters, and Cohan (2020)).

Beltagy, Iz, Matthew E. Peters, and Arman Cohan. 2020. “Longformer: The Long-Document Transformer.” https://arxiv.org/abs/2004.05150.

4 Conclusion

As part of this blog post, we first looked at the difference full-attention with complexity \(O(n^2)\) and sliding window attention. Figure 1

Next, we learnt how to easily perform \(Q.K^T\) using torch.einsum. Finally, we saw that by converting Query \(Q\) and Key \(K\) to chunks, we can easily implement sliding window attention in PyTorch.

Subscribe to Aman Arora's blog:

* indicates required